|
Poslao: 05 Apr 2013 16:00
|
offline
- Mixycami
- Novi MyCity građanin
- Pridružio: 05 Apr 2013
- Poruke: 9
|
Površina osnove valjka je 16Π(pi) .Izračunaj zapreminu tog valjka ako je površina omotača jednaka zbiru površina njegovih osnova.

|
|
|
|
|
Registruj se da bi učestvovao u diskusiji. Registrovanim korisnicima se NE prikazuju reklame unutar poruka.
|
|
|
Poslao: 05 Apr 2013 16:09
|
offline
- vasa.93

- Moderator foruma

- Pridružio: 17 Dec 2007
- Poruke: 14824
- Gde živiš: Niš
|
Površina osnove valjka se računa kao r²Π. Odatle je poluorečnik osnove jednak 4.
Kako su površine omotača i zbir površina osnova jednake, odatle se može izračunati visina valjka. Zbir površina osnove je 16Π + 16Π i to je 32Π. Površina omotača valjka se računa po obrascu M=2rΠH. Odatle možeš da izračunaš H. Zatim dobijenu visinu pomnožiš sa površinom osnove i dobiješ zapreminu.
|
|
|
|
|
|
|
Poslao: 06 Apr 2013 08:55
|
offline
- Mixycami
- Novi MyCity građanin
- Pridružio: 05 Apr 2013
- Poruke: 9
|
Napisano: 05 Apr 2013 17:05
vasa.93 ::Površina osnove valjka se računa kao r²Π. Odatle je poluorečnik osnove jednak 4.
Kako su površine omotača i zbir površina osnova jednake, odatle se može izračunati visina valjka. Zbir površina osnove je 16Π + 16Π i to je 32Π. Površina omotača valjka se računa po obrascu M=2rΠH. Odatle možeš da izračunaš H. Zatim dobijenu visinu pomnožiš sa površinom osnove i dobiješ zapreminu.
Hvala puno riješila sam zadatak.Poslaću kasnije još jedan koji je bio za peticu.
Dopuna: 06 Apr 2013 8:55
Dužina jedne stranice pravougaonika je 24cm, a druga stranica je za 16cm kraća od njegove dijagonale.Prava p leži u ravni pravougaonika i paralelna je njegovoj manjoj stranici.Izračunaj zapreminu tijela dobijenog obrtanjem pravougaonika oko prave p,ako jecrastojanje te prave od manje stranice jednako 6cm.
Može pomoć??
|
|
|
|
|
|
|
Poslao: 06 Apr 2013 10:33
|
offline
- smorena
- Zaslužni građanin

- Pridružio: 14 Mar 2012
- Poruke: 566
|
Pokusaj sama da uradis. Nacrtas pravougaonik.
stranica a=24cm, b=d-16, i imas nepoznato d pa primjeni Pitagorinu teoremu na pravougli trougao i odmah dobijas stranice d i b.
Dalje evo ukratko kao da radis:

Nadam se da ce ti ovo pomoci, i da ces uspjeti sama detaljno da uradis. 
|
|
|
|
|
|
|
Poslao: 19 Apr 2013 13:11
|
offline
- Mixycami
- Novi MyCity građanin
- Pridružio: 05 Apr 2013
- Poruke: 9
|
Evo jedan zadatak iz matematike. Pomagajte hitno je.
Ako se ivica kocke poveća za 1cm, novodobijena kocka ima površinu za 3,66 dm (kvatratnih) veću od prvobitne. Kolika je zapremina kocke?
|
|
|
|
|
|
|
Poslao: 19 Apr 2013 13:57
|
offline
- smorena
- Zaslužni građanin

- Pridružio: 14 Mar 2012
- Poruke: 566
|
Evo postupka, nadam se da nisam nesto pogrijesila u racunu. Ti na osnovu ovoga sam probaj da uradis (tako ces i sam znati ako ti nekada bude neki slican), pa provjeri.
Imas formulu za zapreminu kocke, i sve jedinice mjere trebaju da su ti iste (ovdje sam u dm pretvarala). Stranica druge kocke je za 1cm duza od prve, tj a1=a+0,01dm. tj:
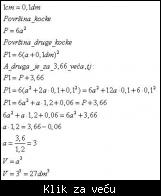
|
|
|
|
|
|
|
Poslao: 19 Apr 2013 20:39
|
offline
- Mixycami
- Novi MyCity građanin
- Pridružio: 05 Apr 2013
- Poruke: 9
|
Napisano: 19 Apr 2013 17:18
Hvala vam puno!
Ne umijem ni ovaj da uradim.
Izvodnica kupe je dva puta veća od prečnika njene osnove. Naći odnos površine omotača kupe i površine njene osnove.
Dopuna: 19 Apr 2013 20:38
Poslaću još jedan, a je l‘ možete da uradite ovaj prethodni?
Dopuna: 19 Apr 2013 20:39
 :loK :loK  ol: ol:
|
|
|
|
|
|
|
Poslao: 19 Apr 2013 21:45
|
offline
- imho

- Građanin
- Pridružio: 20 Nov 2012
- Poruke: 124
- Gde živiš: Belgrade, Serbia
|
M=πrs
M - površina omotača kupe;
s - izvodnica kupe;
r - poluprečnik osnove kupe
s=2r ⇒ M=2πr²
Površina osnove kupe:
B=πr²
M:B = (2πr²):(πr²) = 2:1
|
|
|
|
|
|
|
Poslao: 24 Apr 2013 16:11
|
offline
- Mixycami
- Novi MyCity građanin
- Pridružio: 05 Apr 2013
- Poruke: 9
|
Napisano: 24 Apr 2013 15:02
Hitnoo.
1.Dvije paralelne ravni sijeku loptu po krugovima čiji su obimi O1=14Πcm i O2=40Πcm. Izračunaj rastojanje centra lopte od tih ravni, ako je površina lopte jednaka 2500cm.
Dopuna: 24 Apr 2013 15:12
Parni kotao oblika valjka zatvoren je i završava se sa obje strane poluloptama. Kolika je zapremina toga kotla, ako je dugačak 4m, a prečnik mu je 90cm.
Dopuna: 24 Apr 2013 15:13
Pomagajteee hitno je.
Dopuna: 24 Apr 2013 16:11
Je li moguće da niko ne umije da ga uradi, molim Vas pomagajteee!
|
|
|
|
|
|
|
Poslao: 24 Apr 2013 17:18
|
offline
- imho

- Građanin
- Pridružio: 20 Nov 2012
- Poruke: 124
- Gde živiš: Belgrade, Serbia
|
Mixycami ::1.Dvije paralelne ravni sijeku loptu po krugovima čiji su obimi O1=14Πcm i O2=40Πcm. Izračunaj rastojanje centra lopte od tih ravni, ako je površina lopte jednaka 2500cm.
Evo slike (koju si, uostalom, mogla i sama da nacrtaš), sa nje se sve vidi...

Iz formule P=4πR² odrediš poluprečnik lopte R na osnovu poznate površine lopte P, a zatim na osnovu formule O=2πr odrediš i poluprečnike r₁ i r₂ krugova čiji su obimi O₁ i O₂.
Na kraju primenom Pitagorine teoreme na trouglove △OAA' i △OBB' nađeš dužine OA i OB, koje predstavljaju ono što se u zadatku traži – rastojanje centra lopte od tih ravni.
|
|
|
|
|
|















