Neki poznatiji algoritmi, objasnjenje i implementacije

• 4Ovo se svidja korisnicima: mcrule, bocke, Ričard, 90.42
  
  Registruj se da bi pohvalio/la poruku!

Dakle, počinjemo sa pretraživanjem:
Pod pretraživanjem se podrazumeva nalaženje indeksa člana nekog niza čija je vrednost jednaka traženoj vrednosti. Postoji više načina pretrage, ovde ću napisati jedan sporiji, radi u vremenu O(n) i jedan brži O(log k) gde je k (nepoznati) izabran broj.
O složenosti algoritama, detlajnije ovde

Sporo pretraživanje:
Linearno pretraživanje:
Pod linearnim pretraživanjem podrazumevamo prolazak kroz čitav niz i upoređivanjem svakog elementa sa traženom vrednošću. Niz koji ima n elemenata u najgorem slučaju će napraviti n poređenja(Zato mu je složenost O(n)). Algoritam je veoma prost, ali i manje efikasan na velikim nizovima.
Algoritam:
-napravi petlju koja se kreće od prvog do poslednjeg člana niza
- Za svaki element u nizu proveriti da li je jednak traženoj vrednsoti.
-Ukoliko jeste, sačuvaj njegov index, i prekini pretragu
-U suprotnom, nastavi dalje.
-kada napusti petlju, vrati negativan broj kao znak da nije nađen index.
Implementacija u C-u:
int linearna_pretraga(int *a, int duzina_niza, int vrednost) { for(int i = 0 ; i < duzina_niza ; i++) if(a[i] == vrednost) return i; return -1; }

-------------------------------------------------------------------
Brze pretrazivanje:
Binarna pretraga:
Binarna pretraga je brža i efikasnija od linearne pretrage. Zasniva se na ideji da se u svakom koraku odbaci polovina mogućnosti. Kako?
Pitamo da li je tražena vrednost jednaka srednjem elementu niza. Ukoliko jeste vratimo njegov index, u suprotnom ako je element manji(veći) onda niz polovimo tako da taj srednji član postane gornja(donja) granica i nastavimo postupak. Da bi smo mogli efikasno da primenimo algoritam, niz MORA da bude sortiran.
Primer:
Dat je niz brojava 1,2,3,4,5 ..... 60.
Recimo da treba da proverimo da li se medju njima nalazi broj 47.
Da bi smo to uradili linearnom pretragom mi moramo 47 puta da napravimo poredjenje. Da bi smo to uradili binarnom pretragom.... sad cemo da vidimo:
Pre svakog ovog koraka pitamo da li je broj jednak toj srednjoj vrednosti, ako jeste našli smo ga, u suprotnom pratimo korake:
1.Da li je broj veci od 30? -Jeste. -Razmatramo brojeve od 30-60
2. Da li je broj veci od 45? -Jeste -Razmatramo brojeve od 45 - 60
3. Da li je broj evci od 52? -Nije -Razmatramo brojeve od 45-52
4. Da li je broj veci od 48? Nije -Razmatramo brojeve od 45-48
5. Da li je broj veći od 46? Jeste -Razmatramo brojeve 46-48
6. Pitamo dali je broj jednak sa 47. Jeste - Vratimo njegovu vrednost.

Šta ukoliko ne bi smo znali koliko ima članova u nizu, pa ne možemo da tražimo srednju vrednost.
Jednostavno, uporedjivaćemo broj sa stepenom dvojke sve dok stepen ne postane veći od traženog broja a onda ćemo da primenimo prethodni algoritam jer ćemo imati gornju i donju granicu (gornja je prvi broj koji je prešao vrednost traženog broja, a donja je taj broj/2 )
Algoritam:



Implementacija u C-u:
int binarySearch(int *data, int value, int left, int right) { while (left <= right) { mid = (right-left)/2+left; if (data[mid] == value) return mid; if (value < data[mid]) right = mid-1; else left = mid+1; } return -1; }
Rekurzivna varijanta(nema potrebe za njenim koriscenjem, ali evo implementacije)
int binarySearch(int a[], int value, int left, int right) { if (right < left) return -1; mid = (right-left)/2 + left; if (a[mid] == value return mid; if (value < a[mid]) return binarySearch(a, value, left, mid-1); else return binarySearch(a, value, mid+1, right); }

-------------------------------------
Sortiranje
Jedan od problema u računarstvu jeste uređivanje niza podataka.
Kao što se gore moglo videti kod pretrage da posotji više algoritama koji su različite efikasnosti i složenosti tako i kod algoritama za sortiranje postoje oni koji su manje efikasni i koji su više efikasni.
Ukoliko postoje algoritmi koji su više efikasni, zašto onda koristiti algoritme koji su manje efikasni? Razlog je jednostavan: Nema svrhe koristiti komplikovane algoritme za sortiranje na manje nizove. koji imaju par stotina članova. Kod takvih nizova nećemo primetiti razliku u izvršavanju, a uštedećemo dosta na vremenu potrebnom za implementaciju algortima.
Dakle, ovde će biti opisani sledeći algoritmi:
- Selection sort, radi u vremenu O(n^2)
- Bubble sort, vreme O(n ^2)
- Merge sort, O(n*log n)
- Quick sort, O(n*log n)

Selection sort
Selection sort je jedan od može se reći najprostijih, najintuitivnijih algoritama za sortiranje. Ideja je sledeća:
-Nadjemo najmanji element u nizu
-Zamenimo mu mesto sa prvim elementom
-Ponovimo ovaj postupak počevši od sledećeg elementa.
Animacija prikaya kako radi:


Implementacija u C-u:
void selectionSort(int numbers[], int array_size) { int i, j; int min, temp; for (i = 0; i < array_size-1; i++) { min = i; for (j = i+1; j < array_size; j++) { if (numbers[j] < numbers[min]) min = j; } temp = numbers[i]; numbers[i] = numbers[min]; numbers[min] = temp; } }

Bubble sort>
Bubble sort je jedan od najstarijih, ali i najsporijih algoritama za sortiranje.
Ideja: Poredi svaki element sa prvim do sebe i ukoliko je potrebno menja im mesta.
Postupak se ponavlja sve dok ne prodje kroz celu listu bez zamena, odnosno sve dok ne postane sortiran.
Ovaj algoritam generalno važi za najnefikasniji algoritam. U najboljem slučaju kada je niz već sortiran potrebno mu je vreme O(n) da bi se izvršio, u suprotnom O(n^2).
Primer kako radi, preuzeto sa wikipedije
Let us take the array of numbers "5 1 4 2 8", and sort the array from lowest number to greatest number using bubble sort algorithm. In each step, elements written in bold are being compared.

First Pass:
( 5 1 4 2 8 ) \to ( 1 5 4 2 8 ) Here, algorithm compares the first two elements, and swaps them.
( 1 5 4 2 8 ) \to ( 1 4 5 2 8 )
( 1 4 5 2 8 ) \to ( 1 4 2 5 8 )
( 1 4 2 5 8 ) \to ( 1 4 2 5 8 ) Now, since these elements are already in order, algorithm does not swap them.
Second Pass:
( 1 4 2 5 8 ) \to ( 1 4 2 5 8 )
( 1 4 2 5 8 ) \to ( 1 2 4 5 8 )
( 1 2 4 5 8 ) \to ( 1 2 4 5 8 )
( 1 2 4 5 8 ) \to ( 1 2 4 5 8 )
Now, the array is already sorted, but our algorithm does not know if it is completed. Algorithm needs one whole pass without any swap to know it is sorted.
Third Pass:
( 1 2 4 5 8 ) \to ( 1 2 4 5 8 )
( 1 2 4 5 8 ) \to ( 1 2 4 5 8 )
( 1 2 4 5 8 ) \to ( 1 2 4 5 8 )
( 1 2 4 5 8 ) \to ( 1 2 4 5 8 )
Implementacija u C-u:
void bubbleSort(int numbers[], int array_size) { int i, j, temp; for (i = (array_size - 1); i >= 0; i--) { for (j = 1; j <= i; j++) { if (numbers[j-1] > numbers[j]) { temp = numbers[j-1]; numbers[j-1] = numbers[j]; numbers[j] = temp; } } } }
------------------------------------
Do kraja dana bice postavljeni i quick sort i merge sort

• 0Niko još nije pohvalio poruku.
  Registruj se da bi pohvalio/la poruku!

Svaka čast za ovo. Ovo je odlično štivo za one koji žele da se upuste u svet programiranja. Nadam se da će biti još ovakvih tekstova o algoritmima.

• 0Niko još nije pohvalio poruku.
  Registruj se da bi pohvalio/la poruku!

Fino fino, nadam se da ce se tema dotaci i hash tabela

• 2Ovo se svidja korisnicima: bocke, mcrule
  
  Registruj se da bi pohvalio/la poruku!

Posle duze pauze, sledi nastavak, ubrzo nadam se i sledeci.
U planu su jos hes tabele
Mozda neki geometrijsi algoritmi
- utvrdjivanje da li je tacka unutar mnogougla
- konsturkcija mnogougla
- konveksni omotac

Algebarski algoritmi
- Stepenovanje (vise varijanti)
- Mnozenje matrica (vise varijanti )
- Mnozenje polinoma

Quick sort
Quick sort algoritam za sortiranje niza je jedan od najbrzih algoritama koji danas postoji. Selection sorti i bubble sort koji su gore opisani imaju vreme izvrsavanja O(n^2) (O slozenosti imate link u 4. redu prvog posta u ovoj temi) , dok quick sort ima slozenost O(n log(n))
Ideja algoritma:
- Izaberi jedan clan niza, koji cemo zvati pivot
- Uredi niz tako da svi clanovi koji su manji od pivota budu sa leve strane a svi veci sa desne strane pivota.
- Rekurzivno uradi za levi odnosno desni podniz (u odnosu na pivota)
SLIKA:

Kao sto rekoh, quick sort je jedan od najbrzih algoritama za sortiranje koji su zasnovani na poredjenju (postoje algoritmi za sortiranje koji se ne zasnivaju na poredjenju elemenata, bice kasnije objasnjeni) , ali ukoliko se lose izabere pivot moze se desiti da mu vreme izvrsavanja bude kvadratno, tj. O(n^2) . To je slucaj kada je niz vec sortiran (ukoliko se za pivota uzima prvi clan niza)

Merge sort
Merge sort je algoritam cija je slozenost kao i kod quick sort-a, dakle O(n log(n)) . Ideja je sledeca:
- Ukoliko imamo niz duzine 1 , on je vec sortiran, u suprotnom:
- Podeli niz u dva podniza na pola (ili priblizno pola )
- Rekurzivno sortiraj oba podniza
- Spoj dva sortiraja podniza u jedan
Slika koja prilicno dobro opisuje algoritam :


Pseudo kod (preuzeto sa : wikipedije)
function merge_sort(m)     if length(m) ≤ 1         return m     var list left, right, result     var integer middle = length(m) / 2     for each x in m up to middle          add x to left     for each x in m after middle          add x to right     left = merge_sort(left)     right = merge_sort(right)     if left.last_item > right.first_item          result = merge(left, right)     else          result = append(left, right)     return result function merge(left,right)     var list result     while length(left) > 0 and length(right) > 0         if first(left) ≤ first(right)             append first(left) to result             left = rest(left)         else             append first(right) to result             right = rest(right)     end while     if length(left) > 0         append left to result     else          append right to result     return result

Kratak rezime algoritama za sortiranje
Ovde sam napisao cetiri algoritma za sortiranje (selection sort, bubble sort, quick sort, merge sort ). Koji koristiti? -Zavisi od potrebe. Selection sort i bubble sort su mnogo jednostavniji za implementaciju, za shvatanje, intuitivniji su, ali su sporiji. Ipak, ukoliko znamo da niz nece imati veliki broj clanova, ne treba se muciti i implementirati quick sort ili merge sort, jer korisnik nece primetiti razliku u izvrsavanju.
Na adresi:
http://www.sorting-algorithms.com/
Klikom na neku od slicica videcete animaciju brzine kako radi algoritam. Veoma dobro odradjeno imate nekoliko vrsta nizova koje sortiraju pa mozete pogledati.
Na adresi
http://en.wikipedia.org/wiki/Sorting_algorithm#Comparison_of_algorithms
Imate tabelu prednosti i mana algoritama za sortiranje



Sledeca tema: Strukture podataka

Vektor
Vektor (niz) je niz elemenata istog tipa. Velicina vektora je broj elemenata u nizu i ona je fiksirana (moramo unapred znati koliki je niz u koji smestamo neke podatke). Prednost ove strukture je sto nam ako znamo da se prvi element nalazi na poziciji x, a velicina jednog podaka je k bajtova, onda je n-ti element u nizu na poziciji x+(m-1)k sto nam omogucava jednostavno pristupanje bilo kom elementu za vreme O(1).
Nedostatak ove strukture je sto su mu svi podaci istog tipa i sto se ne moze prosirivati u vreme izvrsavanja programa(nije dinamicki). Ipak, i pored toga u mnogim trenutcima ce biti moguce njegovo koriscenje i treba ga koristiti kad god je to moguce.

Povezana lista

Povezana lista je jedna od dinamickih struktura podataka. Nije neophodno znati koliko ce prostora u memoriji zauzimati, i moze se menjati njena velicina za vreme izvrsavanja programa. Ideja povezane liste je da se podaci zapisuju nezavisno, a da opet budu nekako povezani, tj. povezani preko pokazivaca. Dakle, svaki clan povezane liste ima dva polja: vrednost i pokazivac na sledeci element . Prolazak kroz listu je moguc jedino linearno, odnosno, ako trazimo neki element na k-toj poziciji, mi moramo proci kroz k-1 clanova liste da bi smo dosli do njega, jer ne znamo gde se on tacno nalazi u memoriji. Mana ove strukture je sto zauzima nesto vise prostora u memoriji ( zbog pokazivaca), sporije pristupanje k-tom elementu, ali prednosti su brze upisivanje i brisanje u/iz liste.
Ideja kod ubacivanja novog elementa:
- Nadji poziciju gde treba ubaciti novi element
- Pokazivac njegovog prethodnika kopirati u polje pokazivaca novog podatka, a zatim ga promeniti da pokazuje na novi podatak.

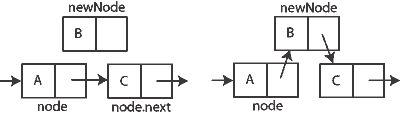
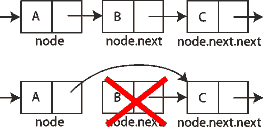
Brisanje ima slicnu ideju (menjanje pokazivaca)



Stabla
Uvod
Stablo je hijerarhijska struktura.
Korensko stablo je skup cvorova i grana koje povezuju cvorove. Jedan cvor je izdvojen, i on je u vrhu, naziva se koren. Svaki cvor osim koren ima svog "oca". U stablu nema ciklusa, jer izmedju svaka dva cvora postoji jedinstven put. Cvor moze da ima "potomke" odnosno "sinove". Dakle, cvorovi koji izlaze iz nekog cvora su njegovi sinovi. Ukoliko cvor nema sinove onda se on zove "list". Maksimalan broj sinova je stepen stabla.
Binarno stablo (o kojem cemo najvise ovde pricati) je stablo ciji je maksimalan stepen dva.
Moguca su dva nacina predstavljanja stabla : implicitno(preko niza) i eksplicitno(preko pokazivaca) .

Binarno stablo pretrage
Kod binarnog stabla, svaki cvor moze imati najvise dva sina(levi i desni). Karakteristika BSP-a je da je svaki cvor veci od svih potomaka u levom podstablu, a manji od svih potomaka u desnom(po dogovoru, jednake mozemo smestati ili u levo ili desno podstablo)
Da ne pricam u prazno, vizuelni prikaz za pocetak:



Operacije kod binarnog stabla:
- Pronalazenje kljuca
- Ubacivanje kljuca
- Brisanje kljuca
Nalazenje:
Ideja je jednsotavna. Krenemo od korena, ukoliko je koren veci od traznog kljuca idemo u levo podstablo, u suprotom u desno. Ponavljamo postupak sve dok ne nadjemo kljuc ili ne naidjemo na NULL (pokazivac na NULL znaci da ne postoji sledeci element, odnosno da nema potomka)
Slicna ideja je i za ubacivanja novog kljuca.
Brisanje kljuca je nesto komplikovanije. Postoji vise slucajeva. Najjednostavnije je brisanje lista, jednostavno sklonimo pokazivac njegovog oca, odnosno postavimo ga na NULL. Drugi slucaj je uklanjanje cvora sa jednim sinom. Takodje, nista tesko, pokazivac od oca cvora koji se brise usmerimo na sina cvora. Ukliko cvor ima oba podstabla , brisanje ide na sledeci nacin: Pronadjemo najlevlji kljuc u desnom podstablu, ili najdesnji u levom. Taj kljuc kopiramo u cvor koji treba izbrisati, a njega brisemo(brisanje lista je trivijalno , prvi slucaj gore)
Sto se tice slozenosti operacija, zavisi od visine stabla, odnosno da li je stablo uravnotezeno ili ne. U najgorem slucaju, slozenost je proporcionalna visini stabla, a ako je uravnotezen, onda je njegova visina log2(n) pa se sve te operacije efikasno izvrsavaju.

AVL stabla
U prethodnom delu videli smo sta su stabla i sta su binarna stabla. Ovde sada pricamo o AVL stablima. AVL stablo je stablo gde se garantuje da slozenost bilo koje od operacija brisanje, ubacivanje novog, trazenje cvora biti u najgorem slucaju O(n log(n)). Zasto je tako? - Zato sto je ideja AVL stabla da se posle svake operacije stablo uravnotezi, tako da mu je visina uvek O(log n) . Poenta je u tome da razlika visina izmedju levog i desnog podstabla svakog cvora bude -1, 0, 1 . Cvor kod kojeg razlika levog i desnog podstabla nije -1,0 ili 1 naziva se kriticni cvor i oko njega se vrse rotacije da bi se uravnotezio.
Postoji vise slucajeva da se pojavi neuravnotezeno AVL stablo.
1) Levo-levo (ako je levo podstablo imalo vecu visinu od desnog i ako je novi cvor ubacen u levo) , slicno i za ostale.
2) Desno-desno
3) Levo-desno
4) Desno-levo
slika koja opisuje rotacije:

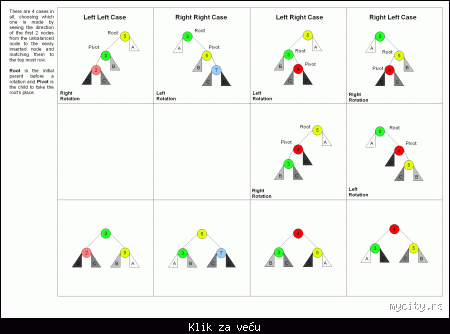
• 3Ovo se svidja korisnicima: N1k0l4, bocke, mcrule
  
  Registruj se da bi pohvalio/la poruku!

Uloguj se preko Facebooka da bi skinuo fajl:

Prilazem program VADer koji smo mi koristili na faksu za vizualizaciju algoritama i struktura podataka:
https://www.mycity.rs/must-login.png
https://www.mycity.rs/must-login.png
https://www.mycity.rs/must-login.png

Program je doduse na nemackom (uobicajeno, s obzirom gde sam studirao), ali postoji dokumentacija na engleskom.

Prilazem i source (Java), ukoliko neko odluci da ga prevede.
Jedini problem sa ponovnim kompajliranjem bi bio sto je program pisan u vreme Java 1.4, pa su potrebne popravke i prepravke da bi mogao da se iskompajlira sa novijim verzijama Jave.

Program se pokrece sledecom komandom:
java AlgoDat
obratiti paznju na mala i velika slova

• 3Ovo se svidja korisnicima: N1k0l4, bocke, mcrule
  
  Registruj se da bi pohvalio/la poruku!

Pogledao sam VADer, nije da se ne snalazim, ali mi nemacki ne ide nikako.

Evo i par drugih linkova za graficke prikaze rada algoritama za sortiranje:



http://www.brian-borowski.com/Sorting/

I lepa kolekcija, sa nekim grafickim prikazima rada i kodovima algoritama:

http://pczenith.com/teorija_algoritama/linkovi_sort_anim.html